Replica exchange nested sampling
Theochem Lunchseminar
24.06.2025
Nico Unglert
Group of Prof. Madsen
Institute of Materials Chemistry
TU Wien

- A primer on nested sampling
- Replica exchange nested sampling
- A few applications
A primer on nested sampling
The nested sampling algorithm
- Initialization: Randomly generate \( K \) walker configurations \( \{ \theta_k \} \)
-
Iterative procedure:
- determine highest energy walker \( \theta_\mathrm{max} \) with energy \( E_{\mathrm{max}} \)
- remove \( \theta_\mathrm{max} \) as a sample
-
sample a new walker configuration uniformly from the region where \( E(\theta) < E_\mathrm{max} \)
NS as an integration algorithm
$$
\begin{align*}
\int \mathrm{d} \theta \; E(\theta)
&\approx \sum_i E(\theta_i) \; w_i \\
\int \mathrm{d} \theta \; e^{-\beta E(\theta)}
&\approx \sum_i e^{-\beta E(\theta_i)} \; w_i
\end{align*}
$$
- Each sample \( \theta_i \) can be assigned a to a volume \(w_i\) in configuration space
- If we had access to these volumes \(w_i\) we could approximate in a Lebesgue fashion:
- NS gives a statistical estimate of volumes \( w_i \)
Sampling new walkers with MCMC
- Initialization: Randomly generate \( K \) walker configurations \( \{ \theta_k \} \)
-
Iterative procedure:
- determine highest energy walker \( \theta_\mathrm{max} \) with energy \( E_{\mathrm{max}} \)
- remove \( \theta_\mathrm{max} \) as a sample
-
sample a new walker configuration uniformly from the region where \( E(\theta) < E_\mathrm{max} \)
$$
\begin{align*}
f_i(\theta) =
\begin{cases}
1 / X_i & \text{if } \; E(\theta) < E_\mathrm{max} \\
0 & \text{otherwise}
\end{cases}
\end{align*}
$$
The most important
NS parameters
-
number of walkers \( K \): higher \( K \) causes
- finer grained sampling (of integral)
- increased likelihood of covering all modes (ergodicity!)
-
walk length \( L \): higher \( L \) causes
- better mode exploration
Cost of nested sampling \( \propto K \cdot L \)
The shortcomings of MCMC
- MCMC struggles for strongly multimodal problems where barrier crossing is necessary
- By nature, NS counteracts this problem due to its collection of \( K \) walkers
- However, to reliably enter very narrow regions, \( K \) needs to be very large!
Replica exchange nested sampling
RENS – the idea
$$
\begin{align*}
f^n_i(\theta) =
\begin{cases}
1 / X^n_i & \text{if } \; E(\theta) < E^n_{i, \mathrm{max}} \\
0 & \text{otherwise}
\end{cases}
\end{align*}
$$
$$
\begin{align*}
f^m_i(\theta) =
\begin{cases}
1 / X^m_i & \text{if } \; E(\theta) < E^m_{i, \mathrm{max}} \\
0 & \text{otherwise}
\end{cases}
\end{align*}
$$
General procedure:
- pick random walkers
- \( \hat\theta^m_i \) from simulation \( m \)
- \( \hat\theta^n_i \) from simulation \( n \)
- swap if
- \( \hat\theta^n_i \) inside \( E^m_{i, \mathrm{max}}\) and
- \(\hat\theta^m_i \) inside \( E^n_{i, \mathrm{max}} \)
A toy model

- two particles in a 1D box with PBC
- Symmetries allow reduction to two degrees of freedom:
- lattice parameter \( a \)
- interparticle distance \( d \)
Pressure RENS
\( P = 0\)
\( P = 2 \)
\( P = 4 \)
- We can now run RENS for different external pressures!
- Below only swap attemps between replica 0 and 1 are shown
Applications of RENS
Applications: toy model
- RENS for 43 pressures between \( P_\mathrm{min}=0 \) and \( P_\mathrm{max}=8.4 \)
- compute heat capacity \( \langle C_P(P, T) \rangle \) and lattice parameter \( \langle a(P, T) \rangle \) with an accurate reference method and compare with independent NS and RENS


$$
\begin{align*}
\int \mathrm{d} \theta \; e^{-\beta E(\theta)}
&\approx \sum_i e^{-\beta E(\theta_i)} \; w_i \\
\langle A \rangle
&= \int \mathrm{d} \theta \; A(\theta) \, e^{-\beta E(\theta)} \\
&\approx \sum_i A(\theta_i) \, e^{-\beta E(\theta_i)} \; w_i
\end{align*}
$$
Applications: toy model


bad
$$
\begin{align*}
\Delta_O(P,T) = \big|O(P,T) - O^{\mathrm{ref}}(P,T)\big|
\end{align*}
$$
- Compute deviation from accurate reference
- RENS allows drastic reduction of \( K \) and \( L \)!
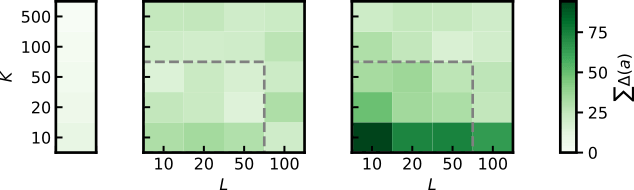
RENS
indep. NS
Applications: Jagla model
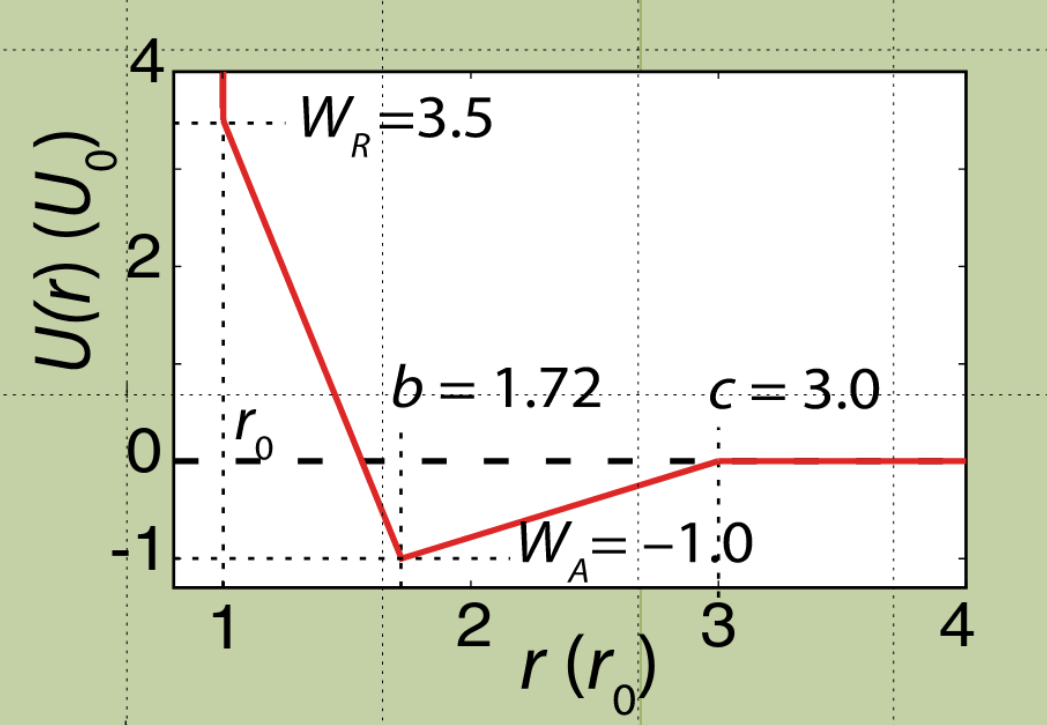
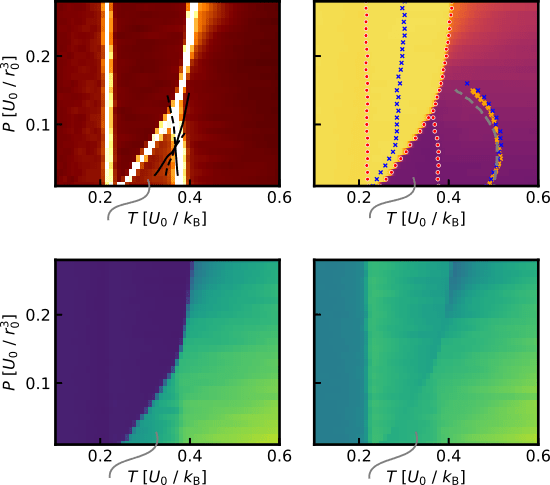
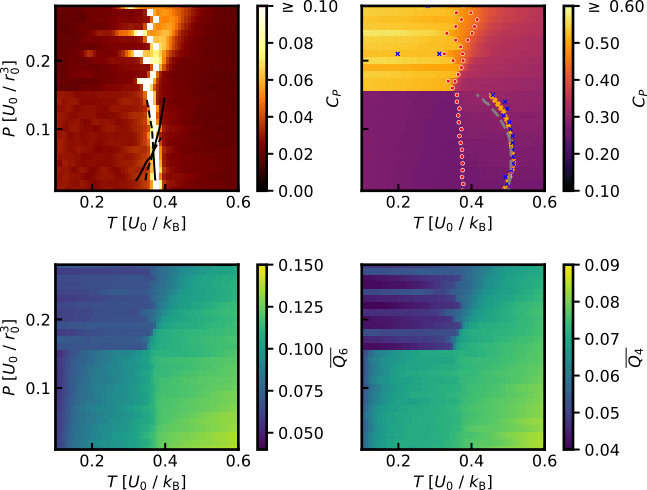
independent NS
RENS

Applications: Silicon NNFF
How to visualize the silicon PES?
- general procedure:
- compute structural order parameter for all ~2400 configurations of NNFF training database
- interpolate enthalpies \( H = U + PV\)
- Here we use parameters derived from the Steinhardt \( Q_4 \) parameter: \( \mathrm{mean}(Q_4) \) and \( \mathrm{std}(Q_4) \)
Independent NS:
- \(N_\mathrm{atoms} = 16\)
- \( K = 600 \)
- \( L = 1000 \)
RENS
- \(N_\mathrm{atoms} = 16\)
- \( K = 600 \)
- \( L = 1000 \)
Applications: Silicon NNFF


RENS
independent NS
Applications: Silicon NNFF

- prediction of proper ground state
- prediction of solid-solid phase transitions
Thank you!
